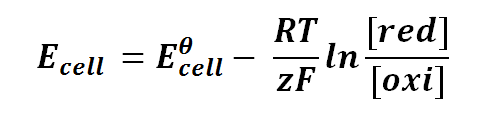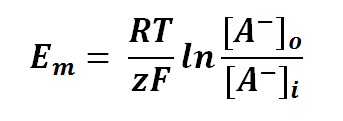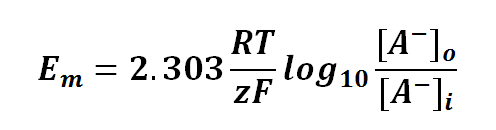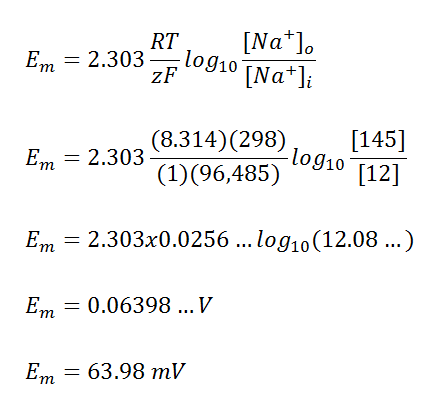Nernst Equation

Nernst Equation is an equation used to calculate the electrical potential of a chemical reaction. In its equilibrium state, the Nernst equation should be zero. It also shows the direct relation between energy or potential of a cell and its participating ions. The equation is proposed by a German chemist, Walther H. Nernst (1864-1941).^[1]

Contents 1 Equation 2 Membrane potential 3 Application 3.1 Using study of frog skin 3.2 Goldman equation 4 See also 5 References & Notes 6 External Links

Equation

Nernst equation can be expressed as follows:

where

E_cell is the half-cell potential difference

E^θ_cell is the standard half-cell potential

R is the universal gas constant; R = 8.314471 J K^-1 mol^-1

T is the thermodynamics temperature, in Kelvin; 0 K = -273.15^oC

z is the number of moles of electrons transferred between cells (defined by the valency of ions)

F is the Faraday's constant; F = 96,485.3415 C mol^-1

[red] is the concentration of ion that gained electrons (reduction)

[oxi] is the concentration of ion that lost electrons (oxidation)

Membrane potential

Main article: Membrane potential

Nernst equation is also can be used to calculate the potential of an ion across the membrane. For potential difference of a membrane, we can manipulate the Nernst Equation as follows:

or

where

E_m is the potential difference of an ion between membranes

R is the universal gas constant; R = 8.314471 J mol^-1

T is the thermodynamics temperature, in Kelvin; 0 K = -273.15^oC

z is the number of moles of electrons transferred between membranes (defined by the valency of ion)

F is the Faraday's constant; F = 96,485.3415 C mol^-1

[A^-]_o is the concentration of ion outside the membrane (in this case is anion, negative charge ion)

[A^-]_i is the concentration of ion inside the membrane (in this case is anion, negative charge ion)

Application

Using study of frog skin

In biochemistry, Nernst equation can be used to calculate the potential difference of ion between membranes. Hans H. Ussing, a Danish scientist, used a frog skin to measure the potential difference of sodium and potassium ions across the membranes with his famous invention, the Ussing chamber.

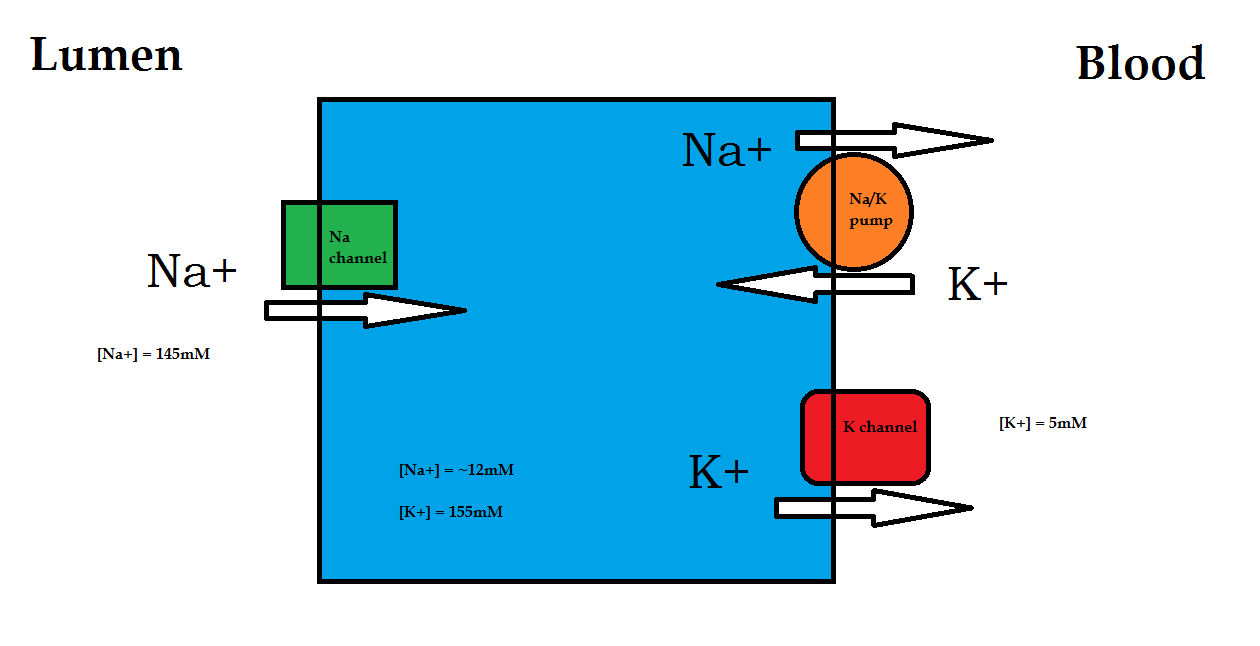
Using model of transepithelial ions absorption ^[2].

For example at the standard condition and temperature of 25^oC (298K), the above sodium ion membrane potential can be calculated as:

Goldman equation

Main article: Goldman equation

In presence of more than one ion, the Nernst equation can be modified into Hodgkin-Katz-Goldman equation or is commonly known as Goldman equation. Goldman equation is proposed by David E. Goldman of Columbia University together with Alan L. Hodgkin and Bernard Katz. It is used to determine the equilibrium potential across a cell's membrane using all of the ions taht can cross the membrane. The Hodgkin-Katz-Goldman equation is essentially a combined Nernst equation, taking into account the permeability's of the many ions present in real cells.

See also

• Membrane potential
  
• Goldman equation
  

References & Notes

1. ↑ http://nobelprize.org/nobel_prizes/chemistry/laureates/1920/nernst-bio.html, The Nobel Prize in Chemistry 1920; Walther Nernst
2. ↑ Diagram based on CMB2003: Cell and Membrane Transport lecture note (2010).

External Links

• The Nernst/Goldman Equation Simulator