Select the format in which molecular structures are to be shown:
- JSmol requires HTML 5.0, and can be slow
- Jmol requires Java to be installed on the client machine, but is sometimes much faster
Format currently selected: HTML5.0_JSmol
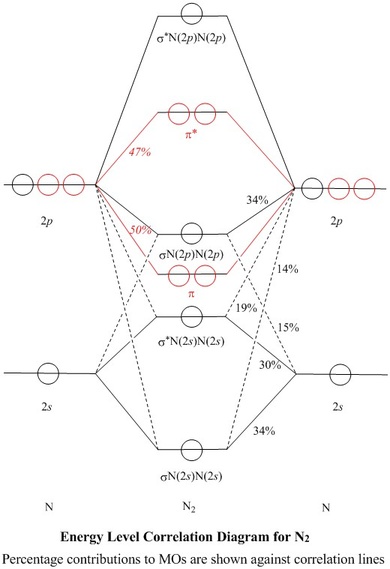
Molecular Orbitals for N2
Jmol models of calculated wavefunctions
To view a model, click in the circle of a molecular orbital in the energy level correlation diagram shown
- Ignore any popup warning and click on the green Continue button which appears
Mouse Control of Models
Left mouse drag to rotate; Shift Left drag up or down to resize;
Shift Right drag or Shift Left drag horizontally to z-rotate;
Right click for menu
Notes
Usage
- The orbitals models are shown in two popup windows, which are reused alternately so that
you can compare one orbital with another
- Contours on a two-dimensional plot correspond to surfaces in three dimensions
- The initial view of a model is with surfaces at ψ = ±0.04
- A radio button is provided to 'Switch contours on'. This shows a
two-dimensional contour plot in the yz plane. This calculation is
slow in the default HTML5.0_JSmol format for the structures:
calculating contours for an orbital takes about 5–10 seconds
in a good browser in a moderately fast PC (in 2018)
- You may see the contour plot better if you 'Switch surfaces off' and click
'Contours coloured'. Black and white contours are provided as the default because
the coloured ones do not show up very well through the coloured surfaces
- If you 'Switch ball and stick off' you can see contours right up to the nuclei,
and where a 2s orbital contributes much you may see its inner lobe with opposite
phase
The Molecule
- N2 is a very stable 10-valence-electron molecule, isoelectronic with
CO and with [CN]–
- The formal bond order of N2 is 3, from about one σ-bond and
two π-bonds
- Its most important property is its lack of reactivity, so that, as the principal
diluent, it can mitigate the dangerous properties of O2 in air
MOs and Natural Atomic Orbitals (NAOs)
| Table of Coefficients and of % of each NAO used,
for each σ–MO |
|---|
| NAO: |
Atom 1 |
Atom 2 |
| N2s |
N2pz |
N2s |
N2pz |
| MO |
coeff. | % used |
coeff. | % used |
coeff. | % used |
coeff. | % used |
| σN(2s)N(2s) |
0.5815 | 34 |
-0.3806 | 14 |
0.5815 | 34 |
0.3806 | 14 |
| σ*N(2s)N(2s) |
0.5491 | 30 |
0.4380 | 19 |
-0.5491 | 30 |
0.4380 | 19 |
| σN(2p)N(2p) |
0.3885 | 15 |
0.5820 | 34 |
0.3885 | 15 |
-0.5820 | 34 |
| σ*N(2p)N(2p) |
0.2476 | 6 |
-0.2605 | 7 |
-0.2476 | 6 |
-0.2605 | 7 |
- The MO models shown on this web page were obtained at the
RMPW1PW91/6–311g(2df) level in a conventional ab initio calculation,
using a Gaussian atomic basis set
- The Gaussian atomic basis set is an approximation to Natural Atomic Orbitals, 2s,
2pz, etc., which are not very amenable to computation
- A Natural Bond Orbital analysis of the resulting MOs produced a set
of NAOs and the coefficients of these needed to make the calculated MOs
- The square of the coefficient, of a NAO in a MO, is the fraction of
the NAO used in that MO
- Most of these squares are shown
as percentages against the correlation lines of the Energy Level
Correlation Diagram
- All of the valence shell NAO contributions
to the σ–MOs are shown in the Table of Coefficients
- Expressed as percentages, all of the AO contributions to a MO should
add up to 100%, and all of the uses of an AO should sum to 100%, since
either an AO or a MO represents exactly one electron
- However, some of the
Gaussian atomic basis maps into core (1s) or higher (3s or 3p)
NAOs, rather than into
valence shell (2s or 2p) NAOs
- While the total of valence shell NAO contributions to e.g.
πy, amounts to 99%, or to
π*y amounts to 95%, the higher energy, empty,
'virtual' MOs are less well accounted for, and consequently are less
likely to be realistic.
Thus, only 26% of σ*N(2p)N(2p)
maps to valence shell NAOs, and the rest to n=3 or n=4 NAOs
- Besides the shortfalls in the total contributions to MOs, the Table
shows also that each NAO is not wholly accounted for. This is
because the rest maps to even higher virtual MOs
Orthogonality of MOs
-
The σ orbitals (black in the Energy Level Diagram)
lie symmetrically across the
π nodes of the πx or πy orbitals
(red), so σ and π MOs do not mix
- Similarly, the πx MO lies symmetrically across
the π node of the πy MO and vice-versa, so
the π orbitals are orthogonal to each other and form a doubly degenerate
set
- In contrast, the nodal planes of the 2pz AOs do not
correspond to an element of symmetry of the molecule, so they do
mix with 2s AOs
- All four of the σ MOs contain both 2s and
2pz contributions from both atoms
The σ System and sp Mixing
These notes may be displayed with or without an explanation of the
values of the LCAO coefficients shown in the Table of Coefficients.
Explanation is currently
on
, as follows:
- Because of the symmetry of the homonuclear molecule, for a
perfect model based only on hydrogen-like valence shell NAOs,
only two independent variables would be required to determine all
16 coefficients
- For example, if the coefficients of the 2s NAO of atom 1
in σN(2s)N(2s) and in
σ*N(2s)N(2s) were known, then
the magnitudes of all of the other 14 coefficients could be derived
from them because of the requirement that each MO represents
exactly one electron, and that each NAO is used exactly once
- Their relative signs are all known because of the requirement
that all MOs are orthogonal to each other
- The coefficients in the first table may be understood using the following mental process
- MOs are considered as linear combinations of AOs
- A linear combination produces the same results, irrespectively of the sequence
in which the terms are added together, so we can consider the process in two steps
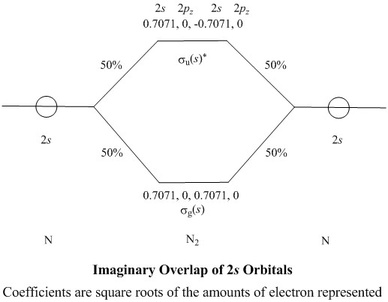
- The first step is entirely imaginary, so it can be perfect:
the intermediate coefficients generated in this step are exactly
known to any desired precision
- The 2s orbitals from each atom are combined to make
a bonding σg(s) and an antibonding
σu(s)* combination
- The g subscript indicates that the value of the wavefunction at any point
is the same as that at a corresponding point on the other side of the centre
of symmetry, which is at the middle of the bond. The u
indicates values of the same magnitude as each other, but of opposite
signs, at such a pair of points
- As there are only two, equal components in σg(s), each
must represent half of an electron,
so the coefficients of the AOs will each be (½)½,
i.e. 0.7071
- In the order of NAOs shown in the first table, the row of coefficients
for σg(s) would
be 0.7071, 0, 0.7071, 0
while for σu(s)* it would
be 0.7071, 0, -0.7071, 0
- Likewise, we can consider bonding,
σg(p) and antibonding
σu(p)* combinations of the
2pz orbitals
- The row of coefficients for σg(p) would
be 0, -0.7071, 0, 0.7071
while for σu(p)* it would
be 0, 0.7071, 0, 0.7071
- Note that, in the bonding combination, the coefficients
have opposite signs because the negative lobe of one
2pz orbital overlaps the positive lobe of the
other, so the overlap integral is negative. A bonding
orbital has a positive contribution to bonding
c1c2S12, where
S12 is the overlap integral
∫φ1φ2dτ
and c1 and c2 are the coefficients,
so if the overlap integral is negative then the
product of the coefficients must also be negative
- Now, in the second stage of our imaginary linear combination,
since they have the same symmetry σg relative to molecular
symmetry, the partial combinations σg(s)
and σg(p) may be further combined to make
the calculated, more bonding and less bonding, combinations
σN(2s)N(2s) and
σN(2p)N(2p)
- For simplicity, the unmixed MO labels are retained on this N2 web
page, even though each σ MO is a mixture of four AOs
- For N2, the names represent the major components in each case
- This time, the amounts of σg(s)
and of σg(p) will not be equal by
symmetry, but should add up so that each MO describes one electron,
and each partial combination is used once altogether, over the
two MOs to which each contributes
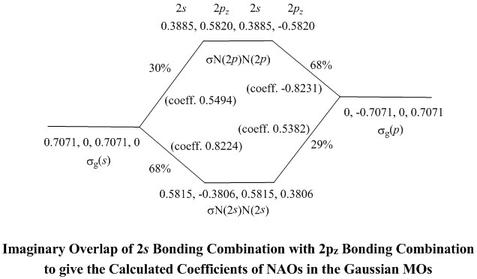
- Their values may be deduced by working back from the optimum
values of coefficients of NAOs in MOs found by the wavemechanical
calculation and presented in the Table of Coefficients
- Thus, the coefficient of the 2s NAO of atom 1 in
σN(2s)N(2s) is shown as 0.5815, so
the coefficient of σg(s) in this MO
is 0.5815/0.7071 = 0.8224, or 67.6%
- Similarly, the coefficient of σg(p)
in this MO comes out as 0.5382, i.e. 29.0%
- The percentages do not quite sum to 100 because of inexact mapping of
NAOs to Gaussian basis set orbitals, as explained above
- For σN(2p)N(2p) the coefficient of
σg(s) is 0.5494 (30.2%) and of
σg(p) is -0.8231 (67.7%),
accounting for the remainder of the σg(s)
and σg(p) partial combinations
- Notice that coefficients of σg(p) are
of opposite sign in making the pair of MOs σN(2s)N(2s)
and σN(2p)N(2p). Just as for making
bonding and antibonding combinations, this is to make the MOs
orthogonal to each other
- The same principles apply to putting together
σu(s)* and σu(p)*
to make the σu MOs
σ*N(2s)N(2s) and
σ*N(2p)N(2p)
- Here, the coefficient of σu(s)*
in σ*N(2s)N(2s)
is 0.7765 (60.3%), and of σu(p)*
is 0.6194 (38.4%)
- Because of the poor mapping of valence shell NAOs to
σ*N(2p)N(2p), it is not worthwhile to
work back from its calculated coefficients. However, we can see
that they should account for the rest of
σu(s)* and σu(p)*,
so, ideally, the coefficients would be about 0.63 (40%) and -0.78 (60%)
| Table of Relative Contributions of
Overlaps to Bonding |
|---|
| MO |
Overlapping AOs |
Overlap integral S |
Contribution c1c2S |
Total for MO |
| Atom 1 | Atom 2 |
| σN(2s)N(2s) |
N2s |
N2s |
0.4795 |
0.1621 |
| σN(2s)N(2s) |
N2s |
N2pz |
0.5075 |
0.1123 |
| σN(2s)N(2s) |
N2pz |
N2s |
-0.5075 |
0.1123 |
| σN(2s)N(2s) |
N2pz |
N2pz |
-0.1797 |
0.0260 |
0.4127 |
| | | | |
| σ*N(2s)N(2s) |
N2s |
N2s |
0.4795 |
-0.1446 |
| σ*N(2s)N(2s) |
N2s |
N2pz |
0.5075 |
0.1221 |
| σ*N(2s)N(2s) |
N2pz |
N2s |
-0.5075 |
0.1221 |
| σ*N(2s)N(2s) |
N2pz |
N2pz |
-0.1797 |
-0.0345 |
0.0651 |
| | | | |
| σN(2p)N(2p) |
N2s |
N2s |
0.4795 |
0.0724 |
| σN(2p)N(2p) |
N2s |
N2pz |
0.5075 |
-0.1147 |
| σN(2p)N(2p) |
N2pz |
N2s |
-0.5075 |
-0.1147 |
| σN(2p)N(2p) |
N2pz |
N2pz |
-0.1797 |
0.0609 |
-0.0961 |
- For the three occupied σ orbitals, for each
of the four pairs of
N—N NAO overlaps, their contribution to bonding
c1c2S12 is shown in the Table of Relative Contributions of
Overlaps to Bonding.
S12 is the overlap integral between them calculated in the NBO
analysis and c1 and
c2 are their LCAO coefficients given in the first Table
- The total contribution to bonding of the three occupied σ orbitals
together is 0.3817, or 47.9% of the total bonding including π bonding
- sp mixing puts p character into σN(2s)N(2s),
making it even more stable. It is now by far the biggest contributor to
bond strength at 51.8% of the total bonding
- Without sp mixing, σ*N(2s)N(2s)
would be an entirely antibonding combination of 2s orbitals,
and σN(2p)N(2p) would be an entirely bonding
combination of 2pz orbitals
- With sp mixing, σ*N(2s)N(2s)
becomes more stable, with a 38% N2pz component
- It is still antibonding with respect to its N(2s) - N(2s) overlap,
but bonding with respect to its N(2s) - N(2pz)
overlaps
- Overall it is now slightly bonding, and contributes 17.1% of the σ
bonding, or 8.2% of the total bonding (including π bonding)
- σN(2p)N(2p) acquires antibonding
N(2s) - N(2pz)
overlaps, making it overall slightly antibonding (a contribution of
-12.1% to total bonding)
- The effects of the weakly bonding σ*N(2s)N(2s)
and the weakly antibonding σN(2p)N(2p)
practically cancel out, leaving the bond order at 3
π Bonding
- Each π or π* orbital should have
only a 2p component from each atom, so each of the four
coefficients should be (½)½,
i.e. 0.7071
- In the present wavemechanical calculation, the values found
were 0.7053 for the π orbitals and ±0.6890 for the
π* orbitals
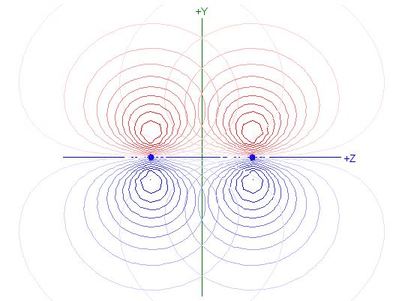
- The overlap integral of 2py orbitals
on atoms 1 and 2 is 0.4178, so the Contribution to Bonding
of this π orbital is 0.2078
- The total contribution of both π orbitals together is
0.4156, or 52.1% of total bonding, including σ bonding
- The π overlap integral is smaller than those for
N(2s) - N(2pz) or N(2s) - N(2s)
overlaps in the σ system (see table), but bigger
in magnitude than the
N(2pz) - N(2pz) overlap integral
- Because the bonding in N2 is dominated by σ
bonding involving s orbital overlaps and by the π
bonding, the equilibrium bond length is such as to favour those
overlaps, but is too short for optimum
N(2pz) - N(2pz) overlap,
as shown in the following contour plot of overlapping 2pz
NAOs for N2:
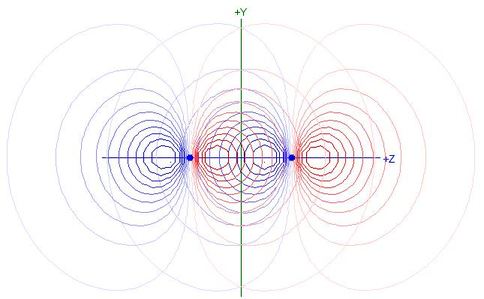
- Each 2pz NAO extends beyond the other nucleus
and hence the nodal plane of the other 2pz NAO
- Products of the two functions in that region are positive, making
the integral less negative
HOMO and LUMOs
- The HOMO of dinitrogen is σN(2p)N(2p)
because the antibonding contribution from sp mixing pushes it
above the π–bonding orbitals in energy
- The LUMOs are the doubly degenerate pair of π* orbitals
- The antibonding nodal surface (approximately the xy
plane) is clearly recognisable in the rotatable model




