| D2h |
E |
C2 (z) |
C2 (y) |
C2 (x) |
i |
σ (xy) |
σ (xz) |
σ (yz) |
| ag |
+1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 |
| b1g |
+1 | +1 | -1 | -1 | +1 | +1 | -1 | -1 |
| b2g |
+1 | -1 | +1 | -1 | +1 | -1 | +1 | -1 |
| b3g |
+1 | -1 | -1 | +1 | +1 | -1 | -1 | +1 |
| au |
+1 | +1 | +1 | +1 | -1 | -1 | -1 | -1 |
| b1u |
+1 | +1 | -1 | -1 | -1 | -1 | +1 | +1 |
| b2u |
+1 | -1 | +1 | -1 | -1 | +1 | -1 | +1 |
| b3u |
+1 | -1 | -1 | +1 | -1 | +1 | +1 | -1 |
For further information on this point group, see
Symmetry at Jacobs University
Select the format in which molecular structures are to be shown:
- JSmol requires HTML 5.0, and can be slow
- Jmol requires Java to be installed on the client machine, but is sometimes much faster
Format currently selected: HTML5.0_JSmol
Molecular Orbitals for Diborane, B2H6
Jmol models of calculated wavefunctions
To view a model,
click in a molecular orbital circle in the energy level correlation diagram shown
- Ignore any popup warning and click on the green Continue button which appears
Mouse Control of Models
Left mouse drag to rotate; Shift Left drag up or down to resize;
Shift Right drag or Shift Left drag horizontally to z-rotate;
Right click for menu
Notes
Usage
- The orbitals models are shown in two popup windows, which are reused alternately so that
you can compare one orbital with another
- Contours on a two-dimensional plot correspond to surfaces in three dimensions
- The initial view of a model is with surfaces at ψ = ±0.04
- A radio button is provided to 'Switch contours on'. This shows a
two-dimensional contour plot
in the xy or xz plane, chosen so that you see some contours for each model.
This is the plane of the screen when the model first appears,
though you may then turn it around
- The calculation of the contour plot is
slow in the default HTML5.0_JSmol format for the structures:
calculating contours for an orbital takes about 5–10 seconds
in a good browser in a moderately fast PC (in 2019)
- You may see the contour plot better if you 'Switch surfaces off' and click
'Contours coloured'. Black and white contours are provided as the default because
the coloured ones do not show up very well through the coloured surfaces
- If you 'Switch ball and stick off' you can see contours right up to the nuclei,
and where a 2s orbital contributes much you may see its inner lobe with opposite
phase
The Molecule
- B2H6 may be considered to be a relatively weak acid-base complex
between two BH3 units
- While
BF3 is a strong Lewis acid, the acidity of boron is reduced
by π-donation from its fluoride ligands, and BF3 exists as a monomer
- No such π-donation is possible for BH3, so even the weakly basic
hydride ligand of another BH3 unit can react to produce the dimer
B2H6, which has two hydride bridges
- Diborane is often given as an example of electron-deficient bonding
- Almost all stable molecules, larger than diatomic, have filled bonding and
non-bonding molecular orbitals, and empty antibonding orbitals
- B2H6 has the correct number of electrons to fit this
prescription, so is not electron-deficient in this sense,
unlike BH3, which has an empty non-bonding orbital
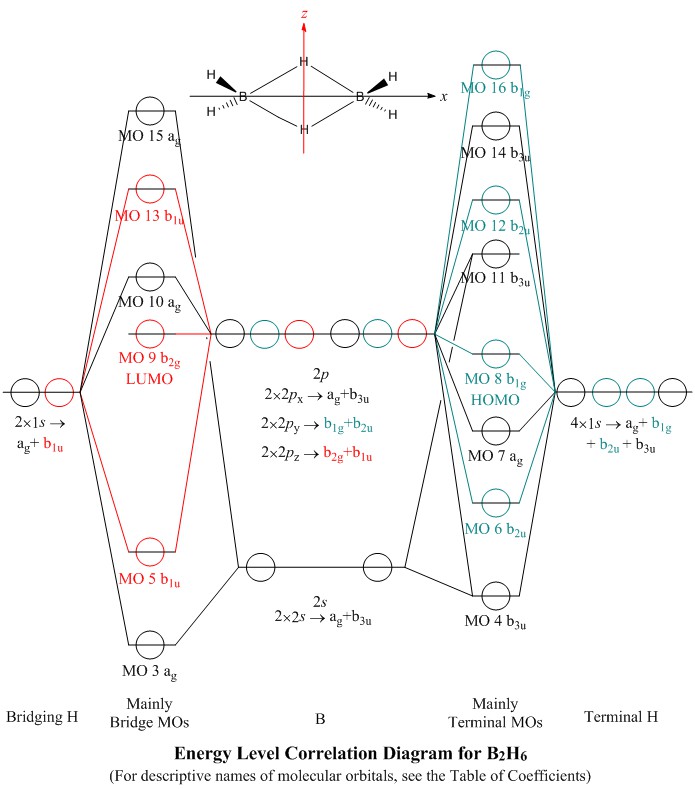
The Energy Level Correlation Diagram
- This is highly schematic: I have presented the calculated MO energy levels
only qualitatively in the order found by the ab initio calculation used
- The MOs are shown with sequential orbital number and group theory representation names,
as brief useful labels
- A character table is provided so that users may check the symmetry properties of the
molecular orbital models which are generated
- Longer titles for the MOs are given in their popup model windows, and in the Table of
Coefficients shown below in the present page: these describe
the main bonding or antibonding nature of the orbital
- Numbering of MOs starts at #3 because the first two MOs counted by an ab initio
package, such as Gaussian, are combinations of the two boron core 1s levels
- MO energy level correlation diagrams in textbooks, for simpler, atom-centred molecules
such as BF3, usually have central atom AOs on one side, ligand AOs on the other,
and the MOs in a central column so that correlation lines may be drawn to indicate the
contributions of AOs to MOs
- Since the situation of bridging hydrogen atoms and of terminal hydrogen atoms in
B2H6 are quite different, I have chosen to present their AOs in
separate columns, which allows two columns of MOs with correlations lines, one for MOs
which involve mainly the hydrogen bridges and one for MOs which involve mainly the
terminal hydrogens
- All of the occupied MOs are involved also in some bonding or antibonding directly
between the boron atoms, but these are generally less important contributions to bonding
than contributions from overlap of boron AOs with hydrogen AOs
- Since hydrogen has only a 1s AO available for bonding, MOs which have a nodal
plane lying through a hydrogen atom are completely non-bonding to it. Thus,
MOs with b1u symmetry (red on diagram) are antisymmetric with respect to
σ (xy) so are non-bonding to the terminal hydrogens, which lie
in the xy plane. These MOs may bond only the bridging hydrogens
- Similarly,
MOs with
b1g or b2u symmetry (green) are antisymmetric with respect to
σ (xz) so are non-bonding to the bridging hydrogens, which lie
in the xz plane. These MOs may bond only the terminal hydrogens
- MOs with symmetry ag (black) contain contributions from both bridging and
terminal hydrogen AOs. I have tried to assign them to the column of MOs corresponding
to their bigger contribution. Thus, MO #7 is assigned to the terminal
bonding column rather than to bridge bonding
Choice of Axes
- B2H6 has D2h symmetry,
having three different C2 axes, one along each Cartesian axis direction
- Which Cartesian axis is assigned to which C2 axis,
of the physical molecule, determines which group theory representation name is given
to each MO
- Thus, the third most stable valence shell MO,
labelled b1u here, where the bridging hydrogen atoms lie along the z–axis
and the x–axis runs through the boron atoms, would be labelled b3u if
the x–axis were chosen to lie through the bridging atoms and the
z–axis through the borons
- This may be seen in the character table for D2h, presented here, where
representation b1u would become representation b3u if the values in
the pair of columns labelled 'C2 (z)' and 'C2 (x)'
were interchanged, and similarly the pair of columns labelled 'σ (xy)'
and 'σ (yz)'
- There does not seem to be a consensus on this, for B2H6, among textbooks and
various web sources
- The energies and appearances of the MOs remain the same: only the symmetry labelling
of the MOs changes when axis assignments are interchanged
- As I have used Gaussian 09 for my ab initio calculation for B2H6,
I am using the axis convention of its 'Standard orientation'
MOs and Natural Atomic Orbitals (NAOs)
| Table of Coefficients and of % of each NAO used,
for each MO |
|---|
| NAO: |
B (2s) |
B (2pz) |
B (2py) |
B (2px) |
H bridging |
H terminal |
| Atom numbers: |
1 3 |
1 3 |
1 3 |
1 3 |
2 4 |
5 6 7 8 |
| MO | |
|---|
| 3 | ag | B(sp_x)_H_bridge |
coeff. size |
0.4578 | 0 | 0 | 0.2509 | 0.3949 | 0.1750 |
| coeff. signs |
+ + | | | - + | + + | + + + + |
| % /NAO |
21.0 | 0 | 0 | 6.3 | 15.6 | 3.1 |
| % /MO |
41.9 | 0 | 0 | 12.6 | 31.2 | 12.3 |
| | | | |
| | | | |
| 4 | b3u | B(sp_x)_H_term |
coeff. size |
0.4009 | 0 | 0 | 0.2864 | 0 | 0.3555 |
| coeff. signs |
+ - | | | + + | | + + - - |
| % /NAO |
16.1 | 0 | 0 | 8.2 | 0 | 12.6 |
| % /MO |
32.1 | 0 | 0 | 16.4 | 0 | 50.6 |
| | | | |
| | | | |
| 5 | b1u | B(p_z)_H_bridge |
coeff. size |
0 | 0.4722 | 0 | 0 | 0.5258 | 0 |
| coeff. signs |
| + + | | | + - | |
| % /NAO |
0 | 22.3 | 0 | 0 | 27.6 | 0 |
| % /MO |
0 | 44.6 | 0 | 0 | 55.3 | 0 |
| | | | |
| | | | |
| 6 | b2u | B(p_y)_H_term |
coeff. size |
0 | 0 | 0.5291 | 0 | 0 | 0.3317 |
| coeff. signs |
| | + + | | | + - - + |
| % /NAO |
0 | 0 | 28.0 | 0 | 0 | 11.0 |
| % /MO |
0 | 0 | 56.0 | 0 | 0 | 44.0 |
| | | | |
| | | | |
| 7 | ag | B(p_x)_H_term |
coeff. size |
0.1698 | 0 | 0 | 0.4700 | 0.1914 | 0.3258 |
| coeff. signs |
+ + | | | + - | - - | + + + + |
| % /NAO |
2.9 | 0 | 0 | 22.1 | 3.7 | 10.6 |
| % /MO |
5.8 | 0 | 0 | 44.2 | 7.3 | 42.5 |
| | | | |
| | | | |
| 8 | b1g | B(p_y)_H_term
HOMO |
coeff. size |
0 | 0 | 0.4760 | 0 | 0 | 0.3688 |
| coeff. signs |
| | + - | | | + - + - |
| % /NAO |
0 | 0 | 22.7 | 0 | 0 | 13.6 |
| % /MO |
0 | 0 | 45.3 | 0 | 0 | 54.4 |
| | | | |
| | | | |
| NAO: |
B (2s) |
B (2pz) |
B (2py) |
B (2px) |
H bridging |
H terminal |
| Atom numbers: |
1 3 |
1 3 |
1 3 |
1 3 |
2 4 |
5 6 7 8 |
| | | | |
| | | | |
| 9 | b2g | B(p_z)_nonbonding
LUMO |
coeff. size |
0 | 0.6706 | 0 | 0 | 0 | 0 |
| coeff. signs |
| + - | | | | |
| % /NAO |
0 | 45.0 | 0 | 0 | 0 | 0 |
| % /MO |
0 | 89.9 | 0 | 0 | 0 | 0 |
| | | | |
| | | | |
| 10 | ag | B(p_x)_H_bridge* |
coeff. size |
0.0225 | 0 | 0 | 0.4014 | 0.3958 | 0.1720 |
| coeff. signs |
+ + | | | + - | + + | - - - - |
| % /NAO |
0.1 | 0 | 0 | 16.1 | 15.7 | 3.0 |
| % /MO |
0.1 | 0 | 0 | 32.2 | 31.3 | 11.8 |
| | | | |
| | | | |
| 11 | b3u | B(sp_x)_B(sp_x)* |
coeff. size |
0.3697 | 0 | 0 | 0.3954 | 0 | 0.0522 |
| coeff. signs |
+ - | | | - - | | - - + + |
| % /NAO |
13.7 | 0 | 0 | 15.6 | 0 | 0.3 |
| % /MO |
27.3 | 0 | 0 | 31.3 | 0 | 1.1 |
| | | | |
| | | | |
| 12 | b2u | B(p_y)_H_term* |
coeff. size |
0 | 0 | 0.3923 | 0 | 0 | 0.3150 |
| coeff. signs |
| | + + | | | - + + - |
| % /NAO |
0 | 0 | 15.4 | 0 | 0 | 9.9 |
| % /MO |
0 | 0 | 30.8 | 0 | 0 | 39.7 |
| | | | |
| | | | |
| 13 | b1u | B(p_z)_H_bridge* |
coeff. size |
0 | 0.3728 | 0 | 0 | 0.3147 | 0 |
| coeff. signs |
| - - | | | + - | |
| % /NAO |
0 | 13.9 | 0 | 0 | 9.9 | 0 |
| % /MO |
0 | 27.8 | 0 | 0 | 19.8 | 0 |
| | | | |
| | | | |
| 14 | b3u | B(sp_x)_H_term* |
coeff. size |
0.3442 | 0 | 0 | 0.2542 | 0 | 0.2944 |
| coeff. signs |
+ - | | | + + | | - - + + |
| % /NAO |
11.8 | 0 | 0 | 6.5 | 0 | 8.7 |
| % /MO |
23.7 | 0 | 0 | 12.9 | 0 | 34.7 |
| | | | |
| | | | |
| 15 | ag | B(s)_H_bridge* |
coeff. size |
0.3876 | 0 | 0 | 0.0391 | 0.2693 | 0.1917 |
| coeff. signs |
+ + | | | + - | - - | - - - - |
| % /NAO |
15.0 | 0 | 0 | 0.2 | 7.3 | 3.7 |
| % /MO |
30.0 | 0 | 0 | 0.3 | 14.5 | 14.7 |
| | | | |
| | | | |
| 16 | b1g | B(p_y)_H_term* |
coeff. size |
0 | 0 | 0.4060 | 0 | 0 | 0.2693 |
| coeff. signs |
| | + - | | | - + - + |
| % /NAO |
0 | 0 | 16.5 | 0 | 0 | 7.3 |
| % /MO |
0 | 0 | 33.0 | 0 | 0 | 29.0 |
| | | | |
| | | | |
| NAO: |
B (2s) |
B (2pz) |
B (2py) |
B (2px) |
H bridging |
H terminal |
| Atom numbers: |
1 3 |
1 3 |
1 3 |
1 3 |
2 4 |
5 6 7 8 |
| | | | |
| | | | |
- The MO models shown on this web page were obtained at the
RHF/3–21G* level in a conventional ab initio calculation,
using a Gaussian atomic basis set
- The Gaussian atomic basis set is an approximation to Natural Atomic Orbitals, 2s,
2pz, etc., which are not very amenable to computation
- A Natural Bond Orbital analysis of the resulting MOs produced a set
of NAOs and the coefficients of these needed to make the calculated MOs
- The valence shell NAO contributions
to the MOs are shown in the Table of Coefficients
- The absolute value of a coefficient is given only once, since all NAOs of a given kind,
e.g. B (2s), are related by the symmetry of the molecule
- This symmetry means that the coefficients may have the same or different signs.
The array of signs is given in the second row of each MO entry, in the order of atom numbers
shown at the head (and foot) of the table
- The relative signs in each array, for a set of NAOs, is the same for all MOs having
a particular group theory representation name, though the array may be multiplied by
–1, so as to generate the antibonding nodes which the make the MOs of a
particular representation orthogonal to each other
- As an example, MO #5 (b1u) has signs + + for the B (2pz)
coefficients and + – for the bridging hydrogen coefficients
- Inspection of the Jmol model for MO #5 shows that this makes it entirely bonding
with respect to both boron-boron and boron-hydrogen interactions, since opposite signs on
the two hydrogen orbitals are required to match the opposite signs of the two lobes of each
p orbital
- MO #13 (b1u) has the same + – sign combination for the H orbitals,
but has – – for the B (2pz) coefficients.
This inverts the boron contribution to this MO and produces the clearly visible antibonding
nodal surfaces
- The square of the coefficient, of a NAO in a MO, is the fraction of
the NAO used in that MO. This, expressed as a percentage, is given in the third row for the MO
- The fourth row is this contribution, before rounding, multiplied by two or four
depending on how many symmetry related instances of this NAO there are. This shows
how much of the MO is involved in bonding or antibonding to this kind of NAO
- Across a row, all of the NAO contributions per MO should
add up to 100%, and, down a column, all of the uses of a NAO should sum to 100%, since
either a NAO or a MO represents exactly one electron
- For the occupied MOs, the sums per MO are in the range 98.0–100.0%, so the
analysis in terms of valence-shell NAOs is valid
- The non-bonding LUMO, MO #9, is only 89.9% described in terms of valence shell NAOs:
the remainder maps onto NAOs from higher shells
- The remaining, higher energy, empty, 'virtual' MOs are less well accounted for,
and consequently are less likely to be realistic. The order of their energies also
varies more, depending on the level of theory used in the wavemechanical calculation, so
may be different in different textbooks etc.
- Down a column, the contributions of each valence shell NAO sums to about 80%. The
rest corresponds to its contributions to higher shell MOs
sp Mixing and MOs with Components which are Antibonding by Symmetry
- Of the boron 2p orbitals, only the 2px orbitals can give
combinations of the same symmetries (ag + b3u)
as do the boron 2s,
and therefore give MOs which are sp mixtures
- For a particular boron atom, B (2px)
and B (2s) appear the same when viewed from the centre of
the molecule, because the nodal planes of B (2px) are not elements
of symmetry of B2H6
- MOs of symmetry b3u, e.g. MO #4, are antisymmetric with respect to
σ (yz), which passes through the bridging hydrogen atoms.
This means not only that they are non-bonding to the bridging hydrogens, but also that they are antibonding
with respect both to B (2s)—B (2s)
and to B (2px)—B (2px) overlaps
They may be bonding or antibonding with respect to B (2s)—B (2px)
overlap, since this is not imposed by the symmetry of the MO
- Similarly, though not involving B (2s) orbitals,
MOs #8 (b1g) and
#9 (b2g) are antisymmetric with respect to the yz plane, so
their B (2p)—B (2p) overlaps also are antibonding by
symmetry
- Of the H (1s)—H (1s) overlaps,
Hbridge—Hbridge is antibonding by symmetry in MO #5
(b1u), as a result of this being antisymmetric with respect to
σ (xy), and
gem–Hterminal—Hterminal is antibonding
in MO #6 (b2u) and MO #8 (b1g), being antisymmetric
with respect to σ (xz)
Three-centre, two-electron Localised Bonding versus the MO Approach
- Each of the two bridging hydride atoms may be considered to be involved in
symmetric 3c—2e bonding,
so in a MO treatment we might expect to find two occupied MOs which are largely bonding
to the bridging hydrogens
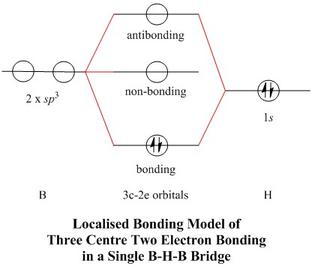
- In fact we find three: MO #3 (ag), #5 (b1u) and #7 (ag), which
contribute to bridge bonding, but MO #7 is nearly non-bonding with respect to bridge bonding
and B—B bonding taken together, so the simple 3c—2e bonding model,
found traditionally in textbooks of Inorganic Chemistry, retains some validity
- The 3c—2e model implies that there should be two empty, non-bonding, boron-centred
orbitals, one for each bridge, accounting for the observed Lewis acidity of
B2H6
- The LUMO, MO #9 (b2g), like the
non-bonding π orbitals of CO2, certainly is of this nature,
though with an antibonding direct interaction between the boron 2pz
orbitals, while the next most stable empty MO, #10, is clearly antibonding to the bridging H atoms
Contributions of Orbitals to Bonding
- The contribution of the overlap of a pair of NAOs φ1 and
φ2 to bonding, in a particular occupied MO, is given by
c1c2S12, where c1
and c2 are their coefficients in that MO, shown in the Table of
Coefficients, and S12 is the overlap integral
∫φ1φ2dτ
- S12 has the same magnitude for all MOs involving this overlap:
it is the coefficients which differ between MOs
- There are 43 such overlaps in a MO with symmetry ag and rather fewer in
the less symmetric other MOs, but most of these are in sets of two, four or, in one case,
eight, with equal values by symmetry, both of magnitude and sign, for all members of the
set
- This reduces the number of different categories of contributions to the 14 shown
in the Table of Contributions, which is divided into two sections for ease of viewing
- Entries for the different directions of the B (2p) orbitals,
px, py or pz, are put together
in the same columns because, for this point group symmetry, only one direction is
involved in any particular MO, and the user may identify this from the title given
to the MO in the Table
- Each column shows one example of the kind of overlap, identified by the atom numbers
in its heading
For this example, the product of coefficients c1c2
and the overlap integral S12 are shown, along with their product, the
contribution to bonding, and the total contribution over all such pairs
- The sign of c1c2 corresponds to the signs of
c1 and c2 respectively in the Table of Coefficients
- For a different overlap in the same set, the sign of this product could be different,
but then the sign of S12 also would be the opposite, so that the sign
of the contribution to bonding would remain the same as in the example given
- The sum of all contributions to bonding is 3.0446, and each non-zero contribution,
for each MO, is shown as a percentage of this, as the final line of each entry
- Of the H—H overlaps, a few individual contributions have a little significance,
but the sum over all MOs of all H—H overlaps is negligible:
the second section of the
Table of Contributions is given only for completeness. The column of totals for
each MO is of use
- It may be seen that MO #3 (ag) contributes 38% of the bonding,
and generally the higher energy MOs contribute progressively less, as might be expected
- The user may observe, however, that there is an anomaly: MO #5 and
MO #6 have energies in the reverse order to that expected from their
total contributions
- These molecular orbitals are calculated to be only 0.0074 Hartrees (19.4 kJmol–1)
apart in energy. The energy inversion is explained by the Natural Bond Orbital
analysis, where the constituent terminal hydrogen 1s orbitals in MO #6
are calculated to be at 0.0456 Hartrees higher energy than the constituent bridging hydrogen NAOs
in MO #5
- Direct bonding between the boron atoms sums to 11.34% of total bonding. With
twelve valence shell electrons, that comes to 1.36 electrons, or about ⅔ of an
electron pair bond
- In addition to this, bonding from the boron atoms to the hydrogen bridges totals
34.94%, or 4.19 electrons. This is just over one electron pair bond per bridge,
or half a bond per contact, in agreement with the 3c—2e bonding model
- The remaining 6.45 electrons, or 53.83% of the bonding, are involved in bonding
between the boron atoms and the terminal hydrogens.
This is about four fifths of an electron pair bond per contact
- For MOs (ag or b3u symmetry) which can involve both
boron 2s and 2px NAOs, their relative overlap integrals
S12 are of interest
- It may be seen from the Table of Contributions that the
B(2s)—B(2s) overlap is bigger in magnitude than the
B(2px)—B(2px) overlap, but the
B(2s)—B(2px) overlap is bigger than either
- This situation is similar to that in
nitrogen, N2
- The π-orientation B(2pz)—B(2pz) overlap,
e.g. in MO #5, is bigger than the B(2px)—B(2px)
overlap, because both lobes of each orbital overlap rather than just one


