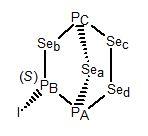
P3Se4I has no symmetry, so it is chiral. The model shown
is of the (S)-enantiomer.
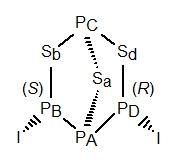
If the sulfur atoms were replaced by selenium either in
β-P4S3I2 or in
α-P4S3I2 (as they can be),
and the PD—I unit
were replaced by a fourth selenium, the result would be P3Se4I.
The 31P and 77Se NMR couplings and chemical shifts for
P3Se4I may be compared with those for
β-P4Se3I2 or for
α-P4Se3I2.
P3Se4I has no symmetry, so it is chiral. The model shown
is of the (S)-enantiomer.
P3Se4I can be made by melting together the elements in the correct stoichiometry, and carefully separating the product from α-P4Se3I2.
It is interesting because it is fluxional on the NMR timescale at room temperature. The iodine becomes attached to PA instead of PB, at the same time as Sed becomes attached to PB instead of PA. The result is the (R)-enantiomer. The enantiomers have exactly the same energy and entropy, so the equilibrium constant for the reaction is 1. This is ideal for observing dynamic NMR, and by computer fitting of a series of 31P NMR spectra measured at different temperatures, a series of rate constants can be found, and hence enthalpies and entropies of activation. Some illustrations of the spectra obtained are shown in the documentation for the program DNMR3.
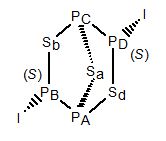
To see a rotatable model of the fluxionality, click on the 'Animation Model' button.
The initial model of the (S)-enantiomer is replaced by a model of the
transition state for the reaction. (The model shown is actually the transition
state for P3Se4Br, rather than P3Se4I,
because that is more suitable for a molecular orbitals calculation.) You may
see that the iodine is connected to both PA and PB in the
transition state, as is Sed. Now switch on the animation with the
radio button provided.
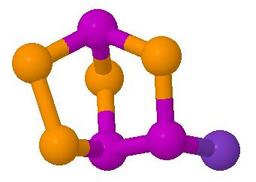The model goes first to the (R)-enantiomer and
then to the (S)-enantiomer, then back again, repeatedly. Try pausing
the animation at each enantiomer in turn, and rotate the model to convince yourself
that one mirror-image has been converted to the other.