Select the format in which molecular structures are to be shown:
- JSmol requires HTML 5.0, and can be slow
- Jmol requires Java to be installed on the client machine, but is sometimes much faster
Format currently selected: HTML5.0_JSmol
Molecular Orbitals for CO
Jmol models of wavefunctions calculated at the
RHF/3–21G*
level
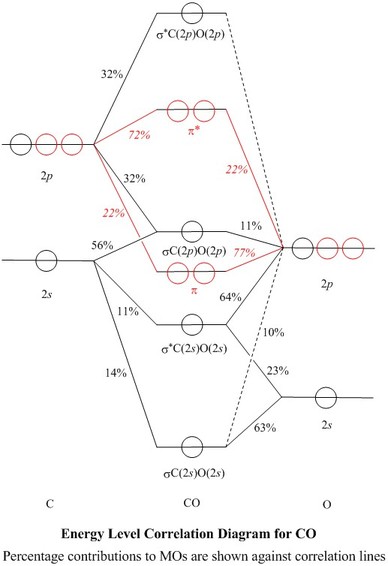
To view a model, click in the circle of a molecular orbital in the energy level correlation diagram shown
- Ignore any popup warning and click on the green Continue button which appears
The results displayed may be switched between those from a low
level of calculation and those from a high level.
- There is rather little difference, either in the orbital models
or in the numbers describing them in the text below, between the two levels of
calculation
- Use the low level for comparison of CO, carbon monoxide, with
CO2, carbon dioxide
- Use the high level for comparison with
N2, nitrogen
The level displayed currently is low
Mouse Control of Models
Left mouse drag to rotate; Shift Left drag up or down to resize;
Shift Right drag or Shift Left drag horizontally to z-rotate;
Right click for menu
Notes
Usage
- The orbitals models are shown in two popup windows, which are reused alternately so that
you can compare one orbital with another
- Contours on a two-dimensional plot correspond to surfaces in three dimensions
- The initial view of a model is with surfaces at ψ = ±0.04
- A radio button is provided to 'Switch contours on'. This shows a
two-dimensional contour plot in the yz plane. This calculation is
slow in the default HTML5.0_JSmol format for the structures:
calculating contours for an orbital takes about 5–10 seconds
in a good browser in a moderately fast PC (in 2018)
- You may see the contour plot better if you 'Switch surfaces off' and click
'Contours coloured'. Black and white contours are provided as the default because
the coloured ones do not show up very well through the coloured surfaces
- If you 'Switch ball and stick off' you can see contours right up to the nuclei,
and where a 2s orbital contributes much you may see its inner lobe with opposite
phase
The Molecule
- CO is a very stable 10-valence-electron molecule, isoelectronic with
[CN]– and with N2, which has a slightly lower
bond dissociation energy than CO
- The formal bond order of CO is 3, from about one σ-bond and
two π-bonds
- Its most important property is burning in air to give CO2,
in the combustion of fossil fuels
- Chemically, its most important reactivity is as a π–acceptor
ligand in metal carbonyl complexes
Polarisation
- More electronegative elements attract their valence shell electrons
more strongly, so their AOs lie at lower energy than those of less
electronegative elements
- In a simple overlap of two AOs, the resulting bonding and antibonding
MOs each resembles most the constituent AO nearest to it in energy
- This means that the bonding MO most resembles the AO of the more
electronegative partner
- Bonding MOs are said to be polarised towards the more electronegative partner atom:
since bonding MOs are filled and antibonding MOs tend to be empty,
this amounts to the classical definition of electronegativity
- An antibonding MO in a simple overlap is composed of those amounts
of AOs not used in making the bonding orbital, so the antibonding MO
most resembles the AO of the less electronegative partner.
We say that antibonding MOs are polarised towards
the less electronegative partner
MOs and Natural Atomic Orbitals (NAOs)
| Table of Coefficients and of % of each NAO used,
for each σ–MO |
|---|
| NAO: |
C2s |
C2pz |
O2s |
O2pz |
| MO |
coeff. | % used |
coeff. | % used |
coeff. | % used |
coeff. | % used |
| σC(2s)O(2s) |
0.3807 | 14 |
0.3188 | 10 |
0.7919 | 63 |
-0.3149 | 10 |
| σ*C(2s)O(2s) |
-0.3352 | 11 |
0.0275 | 0 |
0.4766 | 23 |
0.8017 | 64 |
| σC(2p)O(2p) |
0.7507 | 56 |
-0.5652 | 32 |
-0.0019 | 0 |
0.3331 | 11 |
| σ*C(2p)O(2p) |
-0.3115 | 10 |
-0.5640 | 32 |
0.2514 | 6 |
-0.1814 | 3 |
- The MO models shown on this web page were obtained at the
RHF/3–21G*
level in a conventional ab initio calculation,
using a Gaussian atomic basis set
- This is an approximation to Natural Atomic Orbitals, 2s,
2pz, etc., which are not very amenable to computation
- A Natural Bond Orbital analysis of the resulting MOs produced a set
of NAOs and the coefficients of these needed to make the calculated MOs
- The square of the coefficient, of a NAO in a MO, is the fraction of
the NAO used in that MO
- Some of these squares are shown
as percentages against the correlation lines of the Energy Level
Correlation Diagram
- All of the valence shell NAO contributions
to the σ–MOs are shown in the Table of Coefficients
- Expressed as percentages, all of the AO contributions to a MO should
add up to 100%, and all of the uses of an AO should sum to 100%, since
either an AO or a MO represents exactly one electron
- However, some of the
Gaussian atomic basis maps into core (1s) or higher (3s or 3p)
NAOs, rather than into
valence shell (2s or 2p) NAOs
- While the total of valence shell NAO contributions to e.g.
πy, amounts to 99%, or to
π*y amounts to 94%, the higher energy, empty,
'virtual' MOs are less well accounted for, and consequently are less
likely to be realistic.
Thus, only 51% of σ*C(2p)O(2p)
maps to valence shell NAOs, and the rest to n=3 NAOs
- Besides the shortfalls in the total contributions to MOs, the Table
shows also that each NAO is not wholly accounted for. This is
because the rest maps to even higher virtual MOs
sp Mixing
-
The σ orbitals (black in the Energy Level Diagram)
lie symmetrically across the
π nodes of the πx or πy orbitals
(red), so σ and π MOs do not mix
- Similarly, the πx MO lies symmetrically across
the π node of the πy MO and vice-versa, so
the π orbitals are orthogonal to each other and form a doubly degenerate
set
- In contrast, the nodal planes of the 2pz AOs do not
correspond to an element of symmetry of the molecule, so they do
mix with 2s AOs
- All four of the σ MOs contain both 2s and
2pz contributions from both atoms
- This is in contrast to the 2s and 2pz AOs
of carbon in
carbon dioxide,
which do not mix because there the
nodal plane of 2pz is an element of symmetry
of the molecule. (2s and 2pz AOs on
oxygen in CO2 are like those on carbon or oxygen in CO,
and do mix)
- Without sp mixing, σ*C(2s)O(2s)
would be an entirely antibonding combination of 2s orbitals,
and σC(2p)O(2p) would be an entirely bonding
combination of 2pz orbitals. The formal bond
order would clearly be 3, since bonding due to σC(2s)O(2s)
would be cancelled out by the antibonding effect of
σ*C(2s)O(2s), leaving a net of one
σ bond to go with the two π bonds
- For simplicity, the unmixed MO labels are retained on this CO web
page, even though each σ MO is a mixture of four AOs and in some cases the
AOs in the label are not the most important two
| Table of Relative Contributions of
Overlaps to Bonding |
|---|
| MO |
Overlapping AOs |
Overlap integral S |
Contribution c1c2S |
Total for MO |
| σC(2s)O(2s) |
C2s |
O2s |
0.4454 |
0.1343 |
| σC(2s)O(2s) |
C2s |
O2pz |
-0.3933 |
0.0472 |
| σC(2s)O(2s) |
C2pz |
O2s |
0.5505 |
0.1390 |
| σC(2s)O(2s) |
C2pz |
O2pz |
-0.2189 |
0.0220 |
0.3425 |
| | | | |
| σ*C(2s)O(2s) |
C2s |
O2s |
0.4454 |
-0.0712 |
| σ*C(2s)O(2s) |
C2s |
O2pz |
-0.3933 |
0.1057 |
| σ*C(2s)O(2s) |
C2pz |
O2s |
0.5505 |
0.0072 |
| σ*C(2s)O(2s) |
C2pz |
O2pz |
-0.2189 |
-0.0048 |
0.0369 |
| | | | |
| σC(2p)O(2p) |
C2s |
O2s |
0.4454 |
-0.0006 |
| σC(2p)O(2p) |
C2s |
O2pz |
-0.3933 |
-0.0983 |
| σC(2p)O(2p) |
C2pz |
O2s |
0.5505 |
0.0006 |
| σC(2p)O(2p) |
C2pz |
O2pz |
-0.2189 |
0.0412 |
-0.0571 |
- With sp mixing, σ*C(2s)O(2s)
becomes more stable, with a 64% O2pz component,
which is now its main constituent
- It is still antibonding with respect to its C(2s) - O(2s) overlap,
but bonding with respect to its C(2s) - O(2pz)
overlap
- Overall it is now slightly bonding, and contributes 11% of the σ
bonding, or 5.9% of the total bonding (including π bonding)
- For the three occupied σ orbitals, for each pair of
C—O NAO overlaps, their contribution to bonding
c1c2S12 is shown in the Table of Relative Contributions of
Overlaps to Bonding.
S12 is the overlap integral between them calculated in the NBO
analysis and c1 and
c2 are their LCAO coefficients given in the first Table
- sp mixing puts p character into σC(2s)O(2s),
making it even more stable. It is now by far the biggest contributor to
bond strength at 55% of the total bonding
- In return, σC(2p)O(2p) acquires antibonding
s character, making it overall slightly antibonding (a contribution of
-9.1% to total bonding)
- The effects of the weakly bonding σ*C(2s)O(2s)
and the weakly antibonding σC(2p)O(2p)
practically cancel out, leaving the bond order at 3
HOMO and LUMOs
- The HOMO of carbon monoxide is σC(2p)O(2p)
because the antibonding contribution from sp mixing pushes it
above the π–bonding orbitals in energy
- Its main components are C2s and
C2pz, so it is strongly polarised towards
carbon, and will bond to σ–acceptor species
through carbon, providing that the CO ligand is also acting
as a π–acceptor (the 'synergic effect')
- In the rotatable model, you may see that the oxygen contribution is
just the p orbital, and there is a curved nodal surface between
it and the large C2s part
- The LUMOs are the doubly degenerate pair of π* orbitals
- At 72% C2p, they are clearly polarised towards
carbon, and the antibonding nodal surface (approximately the xy
plane) is clearly recognisable in the rotatable model
- The bonding of carbon monoxide as a π–acceptor
ligand to a π–donor transition metal is often
thought of in terms of the reactivity of the CO π* orbitals
of the free molecule
