Tutorial Using Orbital

Contents

 The Program
 What is an orbital?
 What is a contour plot in Orbital?
 What is a Node?
 Why are there Nodes?
 How do Spherical Nodes in Atomic Orbitals work?
 Which Quantum Numbers Count Nodes in an AO?
 Getting started with an atomic orbital
 Different kinds of atomic orbital node
 Modelling versus Molecular Orbital Theory
 What is an Antibonding Node?
 What are Sigma and Pi Orbitals?
 Getting started with molecular orbitals
 How does Electronegativity Relate to MOs?
 Polarisation
 Using p orbitals
 Pi molecular orbitals
 MOs for HF
 Sigma MOs in linear triatomic molecules
 Pi MOs in linear triatomic molecules
 Pi bonding to a pi-acceptor ligand
 Concluding remarks

The Program

• There are two versions of the computer program needed for this tutorial, both publicly available.   They are very similar in use
1. The stand-alone program ORBITAL for Windows.   This runs only in Windows-based PCs, laptops, etc. It needs to be present on the machine and its output format is fixed and stable
2. The web application ORBITAL for Web Browsers.   This will work on either Windows or non-Windows devices.   So long as it remains available on Newcastle University webpages, it requires no download or installation.   The output format depends on the web browser used and on window size.   Chrome, Safari or Firefox browsers have been found satisfactory, and at least a tablet-sized window is needed for convenience of use


• ORBITAL for Web Browsers is available by clicking the link
  https://teaching.ncl.ac.uk/chemmodels/teaching/orbweb/orbital.html
• Its help is provided as a normal browser popup window


• If you would like a copy of BWT's program ORBITAL for Windows, for your own Windows PC, you can download it from:
http://teaching.ncl.ac.uk/chemmodels/software/
where you can find also instructions for using it
• There is a full introduction to the program, and instructions on how to use it, compiled into its Help menu


• It is probably best to read through the Help from one of these sources, before proceeding with this tutorial.  You should recognise, from the lecture course, all of the ideas discussed in the Introduction to the Help


• In doing these exercises, have on screen at the same time the Orbital window and a web browser window showing this page
• It is suggested that you write down answers to the questions, so that you can review them as you do related exercises later in the tutorial

What is an orbital?

• An orbital is the space-dependent part of a wavefunction which describes an electron in an atom (AO) or in a molecule (MO).   It is a mathematical function
• It may be evaluated anywhere in space
• A surface may be drawn which joins all points at which the wavefunction has a particular value, e.g. ±0.04
• This may be represented in physical or graphical rotatable models, e.g. of a carbon p orbital in CO₂
• Try switching the ball and stick model off, then pull the orbital around, using your mouse (or finger etc. on a tablet)
• If we imagine a planar slice through the atom, and then plot contours for regularly spaced values of the wavefunction in that plane, we can see better how the wavefunction varies with position in space
• In the CO₂ orbital window, try switching contours on, then surfaces off, using the buttons provided.   You have to wait a little while for your computer to do the calculations

What is a contour plot in Orbital?

• Try thinking of a contour plot of rainfall over a geographical region
• Points of equal rainfall are joined by contour lines
• The areas between the contour lines are coloured to make the map easier to read.
• The Met Office uses blue for low rainfall and yellow and red for heavier rain
• Orbital uses the same principle for displaying values of wavefunctions in a plane through the atom(s).   Warm colours from green to dark red are used for positive values and cold colours from cyan to deep blue are for negative values
• Grey is for less positive than green but less negative than cyan.   It therefore includes zero, so nodes are grey, but so is all the nearly empty space

What is a Node?

• A node in an orbital is a surface where the wavefunction changes sign
• In atomic orbitals, nodes may be either planar or spherical
• In MOs there may be planar nodes, if they correspond to mirror planes in the molecule, but most nodes are other, curved shapes

Why are there Nodes?

• There is an infinity of solutions to the wave equation for an electron in an atom or molecule, but we cut this down to a more useful set of orbitals by choosing functions which are orthogonal to each other
• Orbitals are orthogonal if they do not overlap at all, i.e. their overlap integral is exactly zero
• The overlap integral of two orbitals is the sum over all space of the two functions multiplied together at each point in space (to give the dimensions of electron density), multiplied by a small unit of volume (to give dimensions of amount of electron). It measures the fraction of the electron in the overlap
• Two orbitals can have exactly zero overlap if one sits across a node in the other, so each positive product is cancelled out by a corresponding negative product on the other side of the node
• Think of a 1s orbital and a 2p orbital on the same atom.   Every product of the positive 1s orbital with the positive lobe of the 2p orbital is exactly cancelled by the product at a point symmetrically across the node, on the negative side of the 2p orbital, so the two orbitals are orthogonal to each other
• The same applies to two 2p orbitals:   One sits across the nodal plane of the other
• There are just two mutually orthogonal, other 2p orbitals which can sit across the nodal plane of the first, making three in all.   Try sketching a pair of them.   The two nodal planes at right angles divide your sketch into four quarters, so products of the functions at a point in one quarter are exactly cancelled out by products symmetrically across one of the planes
• The nodes are in the wavefunctions in order for them to be orthogonal to each other
• With nodes go quantum numbers, which count the nodes.   From the quantum numbers for an AO, you can work out what nodes, planar or spherical it has, so that you can draw it.   By looking at the contour plot of an AO, you can work out its quantum numbers and hence give it a name, e.g. 3p

How do Spherical Nodes in Atomic Orbitals work?

• The principle is the same as for planar nodes:   a pair of orbitals differing by the presence of a spherical node in one of them, are orthogonal because, on one side of the node, the sum of their products, multiplied by a small element of volume, is cancelled out by the sum of these products on the other side of the node
• The difference is that, unlike the planar node case, corresponding points are not related by a plane of symmetry of the atom, so we cannot say 'the product at this particular point is exactly cancelled by the product at that point'.   We just accept that the constants in the wavefunctions mean that the overlap integral calculation gives a zero result, to within numerical error

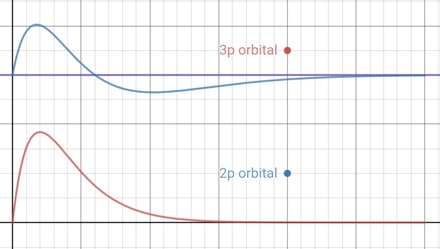
• Here are 2D plots, along the x axis, of the 2p_x and 3p_x orbitals
• The functions used come from the Table of Functions given, and these graphs are very similar to those often shown in textbooks
• You may see that the spherical node in the 3p_x orbital comes part way along the falling curve of the 2p_x orbital
• It is clear that products of the two functions to the right of this value of x will cancel products to the left, but not at all clear that the overall sum of products will come out to zero


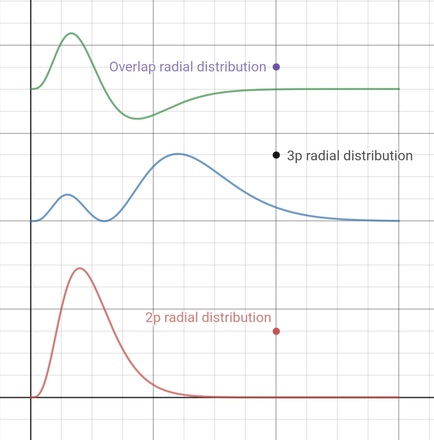
• To obtain relative amounts of electron, we square the wavefunctions to get electron densities, then multiply by the elements of volume.   But the elements of volume get bigger, the further from the nucleus we are:   they are proportional to r², or here, where we are plotting along the x axis, to x², so we multiply the squares of the two functions by x²
• The resulting functions, shown here, are called radial distribution functions
• They show, here, that most of a 3p_x electron is further from the nucleus than most of a 2p_x electron, but its inner lobe penetrates the n=2 shell


• Possibly more interesting in the present context is the top graph, which shows the product of the two functions (which has the dimensions of electron density), multiplied by x² in the same way, to give the radial distribution of overlap
• I find it easy now to believe that the total area under this curve is zero, as required for orthogonality, which it is to within a very small error

Which Quantum Numbers Count Nodes in an Atomic Orbital?

• The Principal Quantum Number n counts the total number of nodes in an AO
• There are n-1 nodes altogether in an AO, not counting the one at infinite distance which you can never see in a plot
• Thus, a 1s orbital has no visible nodes
• An n=2 orbital has one node:   this is spherical in a 2s orbital or planar in a 2p orbital
• The l Quantum Number counts the number of planar nodes in an AO, as follows
• A l=0 orbital has no planar nodes, so is an s orbital
• A l=1 orbital has one planar node, so is a p orbital
• A l=2 orbital has two planar nodes, so is a d orbital
• If l≠0 there are 2l+1 similar orbitals in a set, e.g. three p orbitals
• The remaining n-l-1 AO nodes, if (n-1)≠l, are spherical nodes

Exercise 1: Getting started with an atomic orbital

• Orbital comes up with a contour plot displayed.   Which orbital is this? (If you have changed the plot, refresh the page)
• How many nodes can you see, and of what kind are they (planar or spherical)?
• From your answers to this, write down, for this orbital, the values of the quantum numbers n and l respectively
• Does this correspond to the name you gave it at first?
• The function used is given in the function box for Atom 2
• ^2 means 'raised to the power 2',  i.e. squared
• * means 'times'
• exp means 'e to the power of '
• What does r mean?
• What relationships between x and y make the value of the function zero?
• Write an equation in ordinary, algebraic, form, in which the provided function is set equal to zero
• This is the equation for the nodes:   each of its solutions describes a node
• If the expression in the first parentheses is zero, then the whole l.h.s. is zero, so zoom in on some solutions by writing a new equation with this expression equal to zero. This separates x and y from r
• This is a quadratic equation, so how many solutions does it have?   Write them down
• What does the graph (y versus x) look like, for each solution?
• Are those the nodes which you are seeing in your Orbital window?
• Is the function consistent with your identification of the orbital?
• You can check your answer in the provided Table of Functions
• What is the effect of leaving out the constants A and B shown in the table?


• Start the Animation
• What are you seeing?
• Stop the Animation, then click Redraw Plot
• Move the Animation Speed slider to the left, to about the 1/4 position, or slightly less, then Start Animation again
• Does this help you to see what is happening?
• Try to stop the animation so that the positive and negative lobes are interchanged from the original appearance, which corresponded to the function
• This is clearly the same orbital, at a different instant in time, which is just as valid
• What would matter in an examination would be not which way round you put the signs, but rather that you did label a sketch with the signs, and that you made sure the sign changed each time you crossed a node (and that you marked in all the nodes and labelled them)
• For fun, you can set the animation speed to maximum
• When you have had enough, stop the animation and redraw the plot


• Use the X Range slider or 'spin wheels' or a combination of the two, to set X Range to 5, then click Redraw Plot
• You are plotting contours within an arbitrary window of the xy plane
• You, the chemist, can choose what you want to plot:  no particular window is 'right'
• This window, while it contains a very pretty plot, would not be very informative if you did not know what you are looking at
• Now set the X Range to 30
• What does this tell you about where the electron, described by this function, is to be found?

Exercise 2: Different kinds of atomic orbital node

• Click the dropdown arrow on the function box for Atom 2
• Starting at the top of the dropdown list and working down, try each, in turn, of the remaining functions provided, and identify them from the appearance of their plot as representing particular atomic orbitals
• Stop when you have the 3p orbital on the screen
• X Range should still be at 30 ;  if necessary, reset it to this
• Remember that because all the constants have been removed from these functions, the X scale is arbitrary, and clearly not the same for this 3p function as for the atomic orbital you looked at first.  In reality, they would be of comparable spatial extent
• n is meant to be 3, so there should be two nodes visible in the plot. If not,then you have selected the wrong function
• Identify each node in the plot as spherical or planar, and make a labelled sketch for your records
• Slow animation may again be useful, to emphasise to you the nature of these nodes
• What parts of the function, shown in the Atom 2 function box, produce the nodes which you can see?   The numeric constant in the function is arbitrary, to produce a plot which looks like corresponding plots from real calculations or those in textbooks

Modelling versus Molecular Orbital Theory

• Molecular Modelling is a very important part of modern chemistry, not only for those who work in it as a profession, but also for the very many laboratory research chemists who do modelling calculations to predict or inform their synthetic work or spectroscopy or whatever
• Typically, the user of a modelling package will input or build a starting model, push the appropriate buttons, and the package will optimise the model to a minimum energy
• This will usually involve optimising molecular geometry at some stage
• Chemists are often most interested in predicting reaction energetics or molecular geometry, but if the calculation uses an electronic method ('ab initio' or 'semi empirical'), packages may offer optionally the ability to display calculated MOs
• These are delocalised MOs which extend over the whole molecule
• The HOMO and LUMO orbitals, and possibly MOs near to them in energy, are often bonding in some parts and antibonding in others.   It is useful to able to spot these features, and to see that an orbital may be σ bonding between some atoms but π bonding between others
• Ideas like bonding, non-bonding and antibonding, and the terms σ bonding and π bonding, are part of Molecular Orbital Theory, which is a concept used in Inorganic Chemistry and Organic Chemistry to think about bonding and molecular properties without necessarily doing modelling calculations
• The basic principle, first current in about 1930, is that a MO can be the sum of AOs on the constituent atoms, each multiplied by a scaling down factor, so that the MO represents one electron, as does each of the contributing AOs.   This is the mathematical process of Linear Combination, so the theory is called LCAO-MO Theory
• In this tutorial, the equations, for the overlap of two AOs to give a MO, are provided on a separate web page for easy reference
• Adding together AO functions multiplied by coefficients, and showing a contour plot of the result, is exactly what the Orbital program does, so you may experiment with making your own MOs
• Ab initio modelling packages also do linear combination of atomic functions, though those are more complex and more suited to computational methods than the hydrogenic wave functions considered in the MO Theory concept
• The principles are the same, and, while a good quality ab initio modelling calculation gives us our best idea of what 'reality' 'looks like', the plots produced by Orbital look remarkably similar

What is an Antibonding Node?

• If the product of the coefficients of two AOs in LCAO has the opposite sign to the overlap integral between them, then the contribution to bonding of their overlap in this MO is negative: it is an antibonding contribution
• When just two AOs are overlapping, this will produce a node in the MO, between the two atoms, perpendicular to the line between their nuclei
• We call that an 'antibonding node'.   When we see such a node in the display of a 'real' MO, we know that occupation of this MO would make a negative contribution to bonding between those two atoms
• Just as nodes are present in AOs to make them orthogonal to other AOs, antibonding nodes are present in MOs to make them orthogonal to corresponding bonding MOs

What are Sigma and Pi Orbitals?

• σ (sigma) and π were originally symmetry labels which could be used for classifying MOs in linear molecules such as H₂ or CO₂
• Since the middle of the 20th century, inorganic and organic chemists have borrowed these terms to mean MOs of similar shape to these, in molecules of lower or no symmetry, as well as in linear ones
• We now think of a σ MO as looking like an s AO when viewed along the bond axis between two atoms, while a π MO looks like a p AO
• A π node is a planar node which contains the nuclei of the two atoms concerned
• π nodes are present in MOs to make them orthogonal to corresponding σ MOs

Exercise 3: Getting started with molecular orbitals

• Select the 1s orbital for both Atom 1 and Atom 2
• Change X Range to 15 and Redraw Plot
• What kind of orbital is this?   Describe the orbital as sigma or as pi, and as bonding or as antibonding
• Start a slow animation
• What does this tell you about the number of nodes in this function?   Remember that a nodal surface is where a wavefunction changes sign, not just where it gets to nearly zero
• So were you correct in your naming of the orbital?
• Stop the animation and Redraw Plot
• What is the sign of the overlap integral in this case?
• What sign of the product of the coefficients is required for a bonding combination in this case? (Remember the equation whose last term is the contribution to bonding of an overlap of two AOs in an MO)
• Change the coefficient of Atom 2 to -1
• You may do this by clicking in front of the 1, and typing a - sign, or you may use the 'spin wheels' if provided, or, in Orbital for Web Browsers, by clicking the sign reverse button
• When the coefficient is correct, click Redraw Plot
• What is this new MO?   What new feature does it have?
• What node(s) can you see in this function?
• Can you see why an electron, described by this function, would be less stable than in the AOs taken separately?
• To investigate this, change Left Separation (i.e. between Atom 1 and Atom 2) first to 4, then to 3, doing a Redraw Plot each time, and assessing the result.   The little black dots on the plot are the nuclei
• Zoom in to X Range 10

How does Electronegativity Relate to MOs?

• Draw a simple energy level correlation diagram for one orbital on one atom overlapping with one orbital of the same type, of different energy, on another atom, to give a bonding and an antibonding combination
• A more electronegative atom will attract the electron more strongly, making it more stable, so the lower energy AO belongs to the more electronegative atom
• If we could pull the atoms apart, the bonding MO would go up in energy as the bond got weaker, until it was level with the more stable AO, and the antibonding MO would come down.   Each would become identical to its respective AO
• From this you may gather that the bonding MO looks more like the AO of the more electronegative atom - the classical definition of electronegativity - but the antibonding MO is more like the AO of the less electronegative atom
• This is of central importance in chemistry, because most LUMOs are antibonding, so an incoming nucleophile (or Lewis base) attacking the big end of the LUMO will bond to the less electronegative atom.   Think of hydroxide ion attacking CO₂:   It must attack the less electronegative carbon, because that is where there is a vacant MO to accept its electrons, not the more electronegative oxygens

Exercise 4: Polarisation

• Still with 1s orbitals selected for Atom 1 and Atom 2, change the coefficient of Atom 1 to 1.2 and the coefficient of Atom 2 to 0.8 (both positive now).  Redraw Plot
• Which is the more electronegative atom, the left one (Atom 1) or the right one (Atom 2)?
• Think of a geographical contour map:   a taller hill will usually have a bigger base
• Change the coefficient of Atom 2 to -0.8 and Redraw Plot
• Which is the more electronegative atom now, and how do you know?  Remember the rule explained above

Exercise 5: Using p orbitals

• Select the 2px orbital for both Atom 1 and Atom 2
• Change both coefficients to +1
• Change the Left Separation to 5
• Change the X Range to 15
• Redraw Plot
• What kind of orbital is this?
• Describe the orbital as sigma or as pi, and as bonding or as antibonding
• For what well-known diatomic molecule is this the LUMO?
  • To answer this you will need to draw the energy-level correlation diagram for the first-row homonuclear diatomic molecules:   the one without sp mixing will do:   identify the orbital you have plotted, and count how many electrons are needed for Aufbau, to just leave this MO empty
• Start a slow animation
• What does this tell you about the number of nodes in this function?
• These nodes are of two different kinds:  give names to them
  (Some of these nodes were p orbital nodes in the 2px AOs used.   They no longer correspond to a mirror plane of the molecule, so they are not planar.   They do not have a universally recognised name, but I call them p orbital nodes)
• Is this consistent with your naming of the orbital?
• Stop and Redraw Plot
• What is the sign of the overlap integral in this case?
• What sign of the product of the coefficients is required for a bonding combination in this case? (Remember the equation)
• Compare your answers to those you gave to the same questions in Exercise 3
• Change the settings so that you obtain a plot of a sigma bonding orbital using 2p orbitals
• The antibonding node should have disappeared:   notice the relative signs of the coefficients needed to produce a bonding MO.   This is because of the sign of the overlap integral.   2px orbitals always have their positive lobe pointing in the positive direction along the x axis
• Compare your Orbital contour plot with the output of a 'real' modelling calculation for peroxide ion
• Click on the black circle marked σO(2p)O(2p) in the Energy Level Correlation Diagram, then on the green Continue button if this appears

Exercise 6: Pi molecular orbitals

• Select the 2py orbital for both Atom 1 and Atom 2, and Redraw Plot
• Is this a bonding pi MO, or an antibonding pi MO?
• Set the coefficients so as to make an unpolarised bonding MO, as in the O₂ molecule, and Redraw Plot
• Why is the sign of the product of the coefficients different for a bonding pi MO than for a bonding sigma MO using 2p orbitals?
• Now produce a plot of the LUMO of carbon monoxide, i.e. a polarised antibonding pi MO
• Use coefficients -1.2 and 0.8
• Keep Left Separation as 5, and X Range as 15
• Which atom is carbon?
• At which end of this MO is overlap with a transition metal pi orbital most likely to occur?
• Redraw the plot with Left Separation set successively to 6, 7 and 8
• What do you notice about the shape of the lobes?
• Separation 5 on this (arbitrary) scale is probably about right for the equilibrium bond length of CO
• Compare your Orbital contour plot with the output of a 'real' modelling calculation for CO
• Click on the left-hand red circle marked π^* in the Energy Level Correlation Diagram, then on the green Continue button if this appears

Exercise 7: MOs for HF

• Show the sigma z MO for HF (see Coefficients for HF) as follows
• Select the 1s orbital for Atom 1, with a coefficient of 0.5
• Select the 2px orbital for Atom 2, with a coefficient of -0.8
• In program Orbital, x is used as the molecular axis, rather than the conventional z
• Change Left Separation to 6 (so that you can distinguish the atoms more easily)
• Leave X Range at 15
• Redraw Plot
• Why do the contours at the fluorine end of the orbital spread out further?
• Why are opposite sign coefficients used to make this MO, when same sign coefficients are given in the handout?  (Consider the sign of the overlap integral here, and the one given in the handout, and work out what must be different)
• Change the settings so as to produce a different plot of the same orbital, using same sign coefficients
• What do you gather from this about the sign of overlap integrals?
• Set up a plot of the H 1s - F 2p component of the LUMO of HF, using the coefficients given in the table (rounded to one decimal place)
• You should have an antibonding node as well as a p node, and the orbital should be strongly polarised towards hydrogen

Exercise 8: Sigma MOs in linear triatomic molecules

• Start by adding together a 2p orbital on each of the ligand atoms, but leave out the AO on the central atom for now, as follows
• Select None in the function list for Atom 2
• Select 2px orbitals for both Atom 1 and Atom 3, and coefficients of +1 for both of these
• Set both Left Separation and Right Separation to 6
• Set X Range to 25
• Redraw Plot
• At this distance apart, you see two practically unchanged p orbitals
• With what kind of orbital on the central atom would this combination of ligand orbital coefficients make a fully bonding MO?
• On the basis of your answer to the last question, select the appropriate AO for Atom 2, and set its coefficient so as to make the bonding combination
• To obtain a reasonable representation of polarisation in CO₂, you could make the magnitude of this coefficient 0.8, and the coefficients of the ligand orbitals 1.2
• Compare your Orbital contour plot with the output of a 'real' modelling calculation for carbon dioxide
• Click on the green circle marked σC(2p)O(2p) in the Energy Level Correlation Diagram, then on the green Continue button if this appears
• Redraw Plot
• This plot could also represent one 4p orbital in an octahedral first row transition metal complex overlapping with p orbitals on trans ligand atoms.  The other two 4p orbitals do likewise, giving three degenerate sigma p MOs
• Now change the function for the central Atom 2 to a 1s orbital (here used as an approximation to a 2s orbital in CO₂)
• To make the bonding MO you will now have to change the sign of one of the ligand orbital coefficients
• Which one needs to be changed, Atom 1 or Atom 3, to make the bonding combination?
• Try it, and Redraw Plot
• From this part of the exercise, you can see that different sign combinations, for the coefficients of the ligand orbitals, are needed for the sigma s MO than for the sigma p MO
• This means that s and p AOs on the central atom of a linear triatomic molecule give separate MOs:  they do not mix
• The same applies to octahedral complexes, or to tetrahedral or trigonal planar molecules, for the same sort of reason
• Only in less symmetrical molecules, like bent triatomic or trigonal pyramidal, or on the ligand atoms of molecules, do s and p AOs mix, when they produce the MOs which contain lone pairs
• The other important point to gather from this exercise is that the sigma MOs (not just pi MOs as in Hueckel Theory) extend over all the atoms
• Usually, in ordinary MO theory, there are no localised MOs:  they are all delocalised

Exercise 9: Pi MOs in linear triatomic molecules

• Use 2py orbitals on all three atoms to create a contour plot of an antibonding pi LUMO of CO₂
• Use coefficients of 0.8 and 1.2
• You decide which way round these should be, and what sign they should have
• Left and Right Separations of 5 and X Range 20 give a 'realistic'-looking plot
• You should see a pi node and two antibonding nodes, and it should be apparent that a Lewis base would attack at the carbon atom, at right angles to the molecular axis
• If any of these features are wrong, you have erred.  Revise what you have done and correct the error
• Make a MO setting the Atom 2 function to None, using 2py orbitals on both atoms 1 and 3, and coefficients of +1 for Atom 1 and -1 for Atom 3.  Leave both separations as 5
• This a non-bonding pi orbital
• It is orthogonal to the s or any of the p AOs on the central carbon atom (demonstrate this to your own satisfaction)
• This orbital holds one of the lone pairs on oxygen in CO₂, i.e. it is one of the HOMOs
• Notice that this is one MO, delocalised over both oxygen atoms:  each electron of a lone pair described by this orbital will be partly on each of the two oxygens, but not on the carbon

Exercise 10: Pi bonding to a pi-acceptor ligand

• Imagine that Atom 1 is a transition metal in an octahedral carbonyl complex, Atom 2 is carbon, and Atom 3 is oxygen
• Set up a contour plot of this part of the pi system as follows
• Select the 3dxy orbital for Atom 1, and 2py orbitals for Atoms 2 and 3
• Make the coefficients 1, 1.4, and -1.2 respectively, to take account of polarisation and to create the antibonding node between C and O
• Set Left Separation to 6, Right Separation to 4, to take account of the different atomic radii
• Set X Range to 23
• Redraw Plot
• In reality, the left lobes of this MO would carry on to another OC group

 

Concluding remarks

If you have succeeded in working through all of this tutorial, you should now have a good knowledge of contour plots, of atomic wavefunctions, of nodes in AOs and MOs, of bonding, non-bonding and antibonding sigma or pi MOs, and of matching the signs of coefficients to the signs of overlap integrals.  You should understand polarisation and delocalisation.  You still need to cover radial distribution of AOs and energy level correlation diagrams and orbital occupancy, none of which are dealt with here.  I hope you have enjoyed using my program Orbital and working through this tutorial with it, as much as I have enjoyed creating them.
 
Bruce Tattershall, Chemistry, University of Newcastle